Problem Statement |
|||||||||||||
| A group of freshman rabbits has recently joined the Eel club. No
two of the rabbits knew each other. Today, each of the rabbits
went to the club for the first time. You are given vector <int>s s
and t with the following meaning: For each i, rabbit number
i entered the club at the time s[i] and left the club at
the time t[i].
Each pair of rabbits that was in the club at the same time got to know each other, and they became friends on the social network service Shoutter. This is also the case for rabbits who just met for a single moment (i.e., one of them entered the club exactly at the time when the other one was leaving). Compute and return the number of pairs of rabbits that became friends today. |
|||||||||||||
Definition |
|||||||||||||
|
|||||||||||||
Constraints |
|||||||||||||
| - | s and t will contain between 1 and 50 integers, inclusive. | ||||||||||||
| - | s and t will contain the same number of elements. | ||||||||||||
| - | Each integer in s and t will be between 0 and 100, inclusive. | ||||||||||||
| - | For each i, t[i] will be greater than or equal to s[i]. | ||||||||||||
Examples |
|||||||||||||
| 0) | |||||||||||||
|
|||||||||||||
| 1) | |||||||||||||
|
|||||||||||||
| 2) | |||||||||||||
|
|||||||||||||
| 3) | |||||||||||||
|
|||||||||||||
This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
[Thoughts]
简单的计算区间重合。对于任意两个区间A和B,存在以下四种重合情况:
1. A与B左部重合
2. A与B右部重合
3. A包括B
4. B包括A
假设A的区间是(s[i], t[i]), 而B的区间为(s[j],t[j]),那么重合的判断式如下:
if((s[j] >= s[i] && S[j]<=t[i]) || (t[j]>=s[i] && t[j]<=t[i]) || (s[i] < s[j] && t[i] > t[j]) || (s[i]>s[j] && t[i] < t[j]))
{
count++;
}
显然,这个公式太长了,可以用如下简写版替代:
if( min(t[i],t[j]) - max(s[i], s[j]) ) >==0
[Code]
1: #include <vector>
2: using namespace std;
3: class ShoutterDiv2
4: {
5: public:
6: int count(vector <int> s, vector <int> t);
7: };
8: int ShoutterDiv2::count(vector <int> s, vector <int> t)
9: {
10: int count=0;
11: for(int i =0; i< s.size()-1; i++)
12: {
13: for(int j =i+1; j< s.size(); j++)
14: {
15: if(min(t[i],t[j]) - max(s[i], s[j])>=0)
16: {
17: count++;
18: }
19: }
20: }
21: return count;
22: }
500 points
Problem Statement |
|||||||||||||
| Rabbit went to a river to catch eels. All eels are currently
swimming down the stream at the same speed. Rabbit is standing by
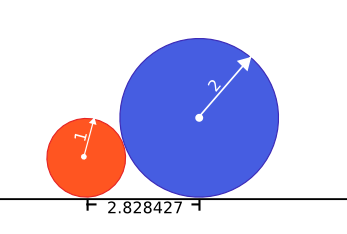
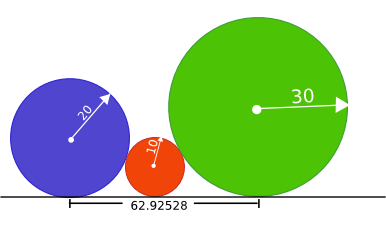
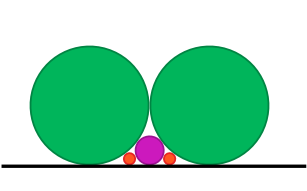
the river, downstream from all the eels. Each point on the river has a coordinate. The coordinates increase as we go down the stream. Initially, Rabbit is standing at the origin, and all eels have non-positive coordinates. You are given two vector <int>s: l and t. These describe the current configuration of eels. The speed of each eel is 1 (one). For each i, the length of eel number i is l[i]. The head of eel number i will arrive at the coordinate 0 precisely at the time t[i]. Therefore, at any time T the eel number i has its head at the coordinate T-t[i], and its tail at the coordinate T-t[i]-l[i]. Rabbit may only catch an eel when some part of the eel (between head and tail, inclusive) is at the same coordinate as the rabbit. Rabbit can catch eels at most twice. Each time he decides to catch eels, he may catch as many of the currently available eels as he wants. (That is, he can only catch eels that are in front of him at that instant, and he is allowed and able to catch multiple eels at once.) Return the maximal total number of eels Rabbit can catch. |
|||||||||||||
Definition |
|||||||||||||
|
|||||||||||||
Constraints |
|||||||||||||
| - | l will contain between 1 and 50 elements, inclusive. | ||||||||||||
| - | Each element of l will be between 1 and 1,000,000,000, inclusive. | ||||||||||||
| - | l and t will contain the same number of elements. | ||||||||||||
| - | Each element of t will be between 0 and 1,000,000,000, inclusive. | ||||||||||||
Examples |
|||||||||||||
| 0) | |||||||||||||
|
|||||||||||||
| 1) | |||||||||||||
|
|||||||||||||
| 2) | |||||||||||||
|
|||||||||||||
| 3) | |||||||||||||
|
|||||||||||||
This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
[Thoughts]
这一题和Leetcode里面买股票的题很类似。
将输入参数转化为Interval,对于任意鱼i,Interval[i].left = t[i], Interval[i].right = t[i]+l[i]。有了Interval数组之后,只要计算该数组在任意时间点上的重合数量,即可确定在该时间点上可以抓到多少鱼。题目已经说了,机器人最多可以抓两次鱼,所以模拟两次抓鱼即可。
[Code]
1: #include <vector>
2: #include <string>
3: using namespace std;
4: class EelAndRabbit
5: {
6: public:
7: int getmax(vector <int> l, vector <int> t);
8: int GetFish(vector <int>& l, vector <int>& t, int time, vector<int>& visited, bool isSecond);
9: };
10: int EelAndRabbit::getmax(vector <int> l, vector <int> t)
11: {
12: vector<int> visited(t.size());
13: int maxCatch=0;
14: for(int i =0;i<t.size(); i++) // t is the left boundary of interval, and l will be right boundary
15: {
16: l[i] = l[i] +t[i];
17: }
18: for(int i =0; i< t.size(); i++)
19: {
20: std::fill(visited.begin(), visited.end(),0);
21: int firstCatch = GetFish(l,t, t[i], visited,false); //first catch
22: int secondCatch=0;
23: for(int j=0;j<t.size(); j++)
24: {
25: if(j== i || t[i]>t[j]) continue;
26: int temp = GetFish(l,t, t[j], visited,true); //second catch
27: if(temp>secondCatch) secondCatch = temp;
28: }
29: if((firstCatch+secondCatch) >maxCatch)
30: {
31: maxCatch=firstCatch+secondCatch;
32: }
33: }
34: return maxCatch;
35: }
36: int EelAndRabbit::GetFish(vector <int>& l, vector <int>& t, int time, vector<int>& visited, bool isSecond)
37: {
38: int temp=0;
39: for(int i =0; i< t.size(); i++)
40: {
41: if(visited[i]) continue; //fish had been caught in first round.
42: if((time >= t[i] && time<=l[i])) // find the overlap interval
43: {
44: if(!isSecond) visited[i] =1;
45: temp++;
46: }
47: }
48: return temp;
49: }
1000 points
Problem Statement |
|||||||||||||
| Rabbit and Eel are playing a board game. The game is played with a
single token on a rectangular board that is divided into a grid of
unit cells. Some cells contain a digit that represents the cost of
placing the token onto that cell. Other cells contain the letter
'x' that represents a blocked cell. It is not allowed to place the
token onto a blocked cell.
Initially, the token is placed on the leftmost cell of the topmost row. (The constraints guarantee that this cell will never be blocked and its cost will always be 0.) Eel starts the game by putting up some walls. Eel may place as many walls as he wants, including none. Each wall must be placed between two adjacent cells in the same column. Once Eel has placed the walls, Rabbit gets to move the token. In each step, Rabbit may move the token one cell left, one cell right, or one cell down. (Note that Rabbit is not allowed to move the token upwards.) Rabbit may only move the token into cells that are not blocked. Each time Rabbit moves the token into a cell, he has to pay the cost associated with that cell. The game ends when Rabbit first moves the token into the bottommost row. The constraints guarantee that this can be achieved if Eel does not place any walls. The game must always be allowed to end. That is, Eel must not place a set of walls that blocks all possible paths to the bottommost row. Rabbit's goal is to minimize and Eel's goal is to maximize the total cost paid by Rabbit during the game. You are given the String[] costs representing the costs of cells: character j of element i of cost is either a digit that represents the cost written in the cell in row i, column j; or it is the letter 'x' that represents a blocked cell. Return the total cost of the game assuming that both Rabbit and Eel play optimally. |
|||||||||||||
Definition |
|||||||||||||
|
|||||||||||||
Constraints |
|||||||||||||
| - | costs will contain between 2 and 50 elements, inclusive. | ||||||||||||
| - | Each element of costs will contain between 1 and 50 characters, inclusive. | ||||||||||||
| - | Each element of costs will contain the same number of characters. | ||||||||||||
| - | Each character of each element of costs will be a letter 'x' or a decimal digit ('0'-'9'). | ||||||||||||
| - | There will be at least one valid path from the leftmost cell of topmost row to a cell in the bottommost row. | ||||||||||||
| - | costs[0][0] will always be '0'. | ||||||||||||
Examples |
|||||||||||||
| 0) | |||||||||||||
|
|||||||||||||
| 1) | |||||||||||||
|
|||||||||||||
| 2) | |||||||||||||
|
|||||||||||||
| 3) | |||||||||||||
|
|||||||||||||
This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
[Thoughts]
DP
首先如果这个题只有Robbit的话,很容易发现这是一个最小路径的DP。此题巧妙处在于做了一个转换,增加了Eel,转换为双人博弈。题目中说了,Eel总是会增加阻碍,让Robbit只能走代价最高的路径。简单的说,如果Eel非常尽职的话,Robbit在每一行只能选择代价最高的那个cell,因为凡是好的路径,必然已经被Eel设置了路障。所以这个题说到底,就是最大路径的DP。具体看code。
[Code]
1: #include <vector> 2: #include <string> 3: using namespace std; 4: class WallGameDiv2 5: { 6: public: 7: int play(vector <string> costs); 8: }; 9: int cost[51][51]; 10: int dp[51][51]; 11: int row, col; 12: int WallGameDiv2::play(vector <string> costs) 13: { 14: //initialize the cost and dp array 15:memset(cost, -1, sizeof(cost));16:memset(dp, -1, sizeof(dp));17: row = costs.size(); 18: col = costs[0].size(); 19: for(int i =0; i< row; i++) 20: { 21: for(int j=0; j< col; j++) 22: { 23: if(costs[i][j] != 'x') 24: { 25: cost[i][j] = costs[i][j]-'0'; 26: } 27: } 28: } 29: dp[0][0] =0; 30: //first row 31: for(int i =1; i< col && cost[0][i]!=-1; i++) 32: { 33: dp[0][i] = (dp[0][i-1] + cost[0][i]); 34: } 35: for(int i =1; i< row-1; i++) 36: { 37: for(int j=0; j<col; j++) 38: { 39: if(dp[i-1][j] == -1) continue; 40: //for each cost i,j, update the value with worst cost 41: int estiCost = dp[i-1][j]; 42: //right 43: for(int k = j; k<col && cost[i][k]!=-1; k++) 44: { 45: estiCost+=cost[i][k]; 46: dp[i][k] = max(dp[i][k], estiCost); 47: } 48: //left 49: estiCost = dp[i-1][j]; 50: for(int k=j; k >=0&& cost[i][k]!=-1; k--) 51: { 52: estiCost+=cost[i][k]; 53: dp[i][k] = max(dp[i][k], estiCost); 54: } 55: } 56: } 57: // last row is special 58: int steps = 0; 59: for(int i =0; i< col; i++) 60: { 61: if(cost[row-1][i] ==-1) continue; 62: steps = max(steps, dp[row-2][i]+cost[row-1][i]); 63: } 64: return steps; 65: }
[Note]
Line 15 & 16
最初的写法是:
memset(cost, -1, sizeof(cost)/sizeof(int));
memset(dp, -1, sizeof(dp)/sizeof(int));
刚开始提交,过不了大数据,翻来覆去的看,也没发现有什么问题。最后拿到visual studio里面debug才发现问题,多了sizeof(int)。对于c++不是特别熟悉呀。