Problem Statement |
|||||||||||||
| NOTE: This problem statement contains images that may not display
properly if viewed outside of the applet. Everybody loves geometry, so here is a geometry problem. You have a few marbles of possibly different sizes. You are given a vector <int> radius that describes the marbles: each element of radius is the radius of one of your marbles. You want to place all marbles onto a straight line that is drawn on the table. Clearly, this makes the problem two-dimensional: we can just view the marbles as circles that will all be touching the line from above. Of course, the marbles cannot overlap, so in our problem no two circles are allowed to overlap. Note that you may place the marbles onto the line in any order, you do not have to preserve the order in which they are given in radius. Additionally, you want to pack the bottoms of the marbles as close together as possible. More precisely: For each marble consider the point where it touches the line. Compute and return the smallest possible distance between the farthest two of those points. (That is, if you imagine the line as going from the left to the right, your task is to minimize the distance between the leftmost and the rightmost of the points where the circles touch the line.) |
|||||||||||||
Definition |
|||||||||||||
|
|||||||||||||
Notes |
|||||||||||||
| - | The returned values must have an absolute or relative error less than 1e-9. | ||||||||||||
Constraints |
|||||||||||||
| - | radius will contain between 2 and 8 elements, inclusive. | ||||||||||||
| - | Each element of radius will be between 1 and 1000000000 (10^9), inclusive. | ||||||||||||
Examples |
|||||||||||||
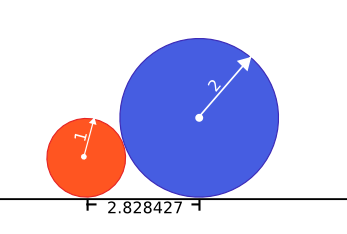
| 0) | |||||||||||||
|
|||||||||||||
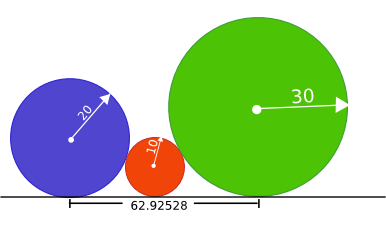
| 1) | |||||||||||||
|
|||||||||||||
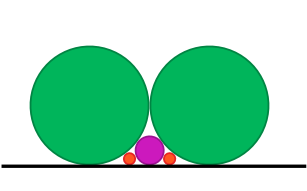
| 2) | |||||||||||||
|
|||||||||||||
| 3) | |||||||||||||
|
|||||||||||||
| 4) | |||||||||||||
|
|||||||||||||
This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
[Thoughts]
分支限界法(branch and bound method)的具体实现之一。以广度优先或者最小损耗的方式搜索解空间,在搜索过程中,不断舍弃非最优解。
一般来说,分支限界法的实现,需要一个有限队列,每次,弹出一个扩展节点,然后基于该扩展节点再搜索,不断加入可能的扩展节点入队,直至队列为空。
但是在此题中,关于圆的排列,缺乏明确的条件在广度优先搜索中淘汰非最优节点。所以,退化为递归+剪枝。
1: #include <string> 2: #include <vector> 3: #include <cmath> 4: using namespace std; 5: class MarblePositioning 6: { 7: struct Circle 8: { 9: double x; 10: int r; 11: }; 12: public: 13: double GetXOfCenter(vector<Circle>& arrange, Circle& added); 14: double GetCurrentLength(vector<Circle>& c); 15: void GetMinArrangement(vector<Circle>& circles, vector<Circle>& arrange, vector<bool>& visited, double& minLen); 16: double totalWidth(vector <int> radius); 17: }; 18: // Get the X coordinate of center of the circle. 19: // Here, need go through all the circles instead of comparing with previous circle only, in case of circle overlap.20: double MarblePositioning::GetXOfCenter(vector<Circle>& arrange, Circle& added) 21: { 22: double x=0; 23: for(int i =0; i<arrange.size(); i++) 24: { 25: // sqrt( (ra+rb)^2 - (ra-rb)^2) 26: double temp = arrange[i].x + 2* sqrt(arrange[i].r*added.r); 27: if(temp>x) x= temp; 28: } 29: return x; 30: }31: // Get the length of current circle queue 32: double MarblePositioning::GetCurrentLength(vector<Circle>& c) 33: { 34: if(c.size() ==0) return 0; 35: return c[c.size()-1].x - c[0].x; 36: } 37: void MarblePositioning::GetMinArrangement(vector<Circle>& circles, vector<Circle>& arrange, vector<bool>& visited, double& minLen) 38: { 39: if(GetCurrentLength(arrange) > minLen) return; // pruning all non-optimization branch 40: if(circles.size() == arrange.size()) 41: { 42: double newLen = GetCurrentLength(arrange); 43: if(newLen < minLen) minLen = newLen; 44: return; 45: } 46: for(int i =0; i < circles.size(); i++) 47: { 48: if(visited[i]) continue; 49: circles[i].x = GetXOfCenter(arrange, circles[i]); 50: arrange.push_back(circles[i]); 51: visited[i] = true; 52: GetMinArrangement(circles, arrange, visited, minLen); 53: arrange.pop_back(); 54: visited[i] = false; 55: circles[i].x =0; 56: } 57: } 58: double MarblePositioning::totalWidth(vector <int> radius) 59: { 60: vector<Circle> sample(radius.size()); 61: for(int i =0; i< radius.size(); i++) 62: { 63: sample[i].r = radius[i]; 64: sample[i].x = 0; 65: } 66: vector<Circle> arrange; 67: vector<bool> visited(radius.size()); 68: double minLen = INT_MAX; 69: GetMinArrangement(sample, arrange, visited, minLen); 70: return minLen; 71: }
[Some Notes]
1. Function GetMinArrangement 的 visited数组是不必要的,可以通过判断circle.x ==0来代替,这里完全是为了可读性。
No comments:
Post a Comment