Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and set.
get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.set(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.
[Thoughts]
首先,对于cache,如果希望有O(1)的查找复杂度,肯定要用hashmap来保存key和对象的映射。对于LRU而言,问题在于如何用O(1)解决cache entry的替换问题。
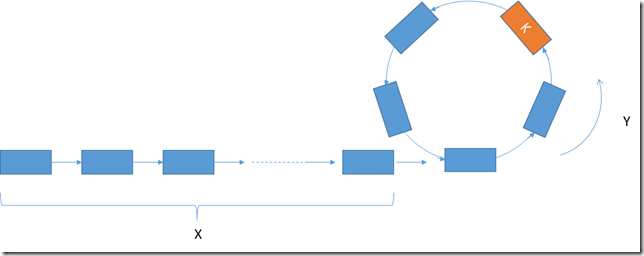
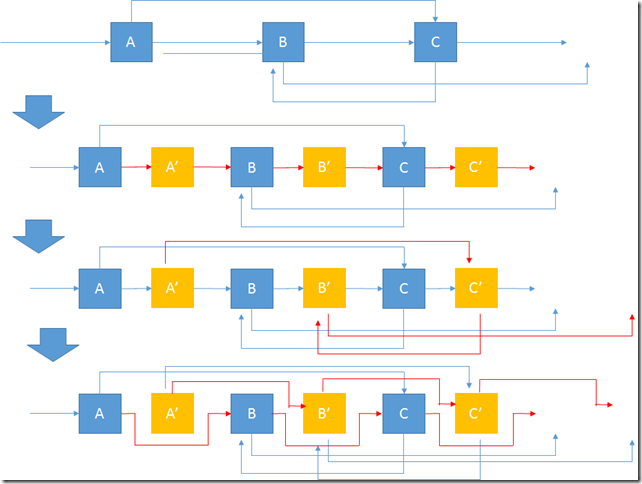
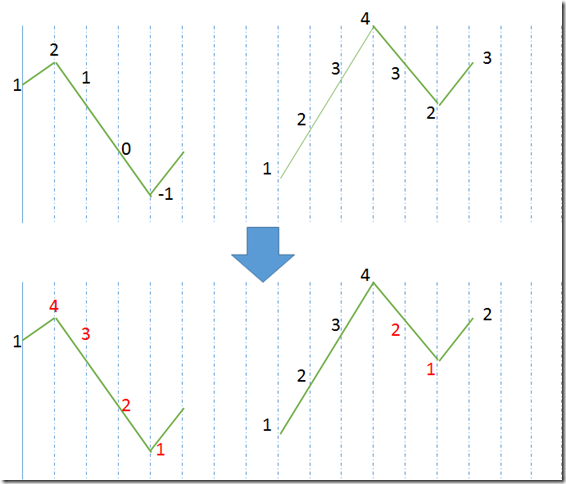
简单的说,cache的存储是一个链表的话,那么只要保证从头到尾的顺序就是cache从新到旧的顺序就好了,对于任何一个节点,如果被访问了,那么就将该节点移至头部。如果cache已满,那么就把尾部的删掉,从头部插入新节点。
所以,需要用到两个数据结构
1. hashmap, 保存key和对象位置的映射
2. list,保存对象新旧程度的序列。不一定是list,也可以用vector,不过list的好处是已经实现了头尾操作的api,vector的话,还要自己写,麻烦。
[Code]
1 class LRUCache{
2 public:
3 struct CacheEntry
4 {
5 public:
6 int key;
7 int value;
8 CacheEntry(int k, int v) :key(k), value(v) {}
9 };
10
11 LRUCache(int capacity) {
12 m_capacity = capacity;
13 }
14
15 int get(int key) {
16 if (m_map.find(key) == m_map.end())
17 return -1;
18
19 MoveToHead(key);
20 return m_map[key]->value;
21 }
22
23 void set(int key, int value) {
24 if (m_map.find(key) == m_map.end())
25 {
26 CacheEntry newItem(key, value);
27 if (m_LRU_cache.size() >= m_capacity)
28 {
29 //remove from tail
30 m_map.erase(m_LRU_cache.back().key);
31 m_LRU_cache.pop_back();
32 }
33
34 // insert in head.
35 m_LRU_cache.push_front(newItem);
36 m_map[key] = m_LRU_cache.begin();
37 return;
38 }
39
40 m_map[key]->value = value;
41 MoveToHead(key);
42 }
43
44 private:
45 unordered_map<int, list<CacheEntry>::iterator> m_map;
46 list<CacheEntry> m_LRU_cache;
47 int m_capacity;
48
49 void MoveToHead(int key)
50 {
51 //Move key from current location to head
52 auto updateEntry = *m_map[key];
53 m_LRU_cache.erase(m_map[key]);
54 m_LRU_cache.push_front(updateEntry);
55 m_map[key] = m_LRU_cache.begin();
56 }
57
58 };