水中的鱼: [TopCoder] SRM 587 DIV 2, 250p, 500p, 1000p, Solution

Problem Statement 250P

You are given two strings: init and goal. Both init and goal contain lowercase letters only. Additionally, init does not contain the character 'z'.
Your goal is to transform init into goal. The only operation you are allowed to do is to insert the character 'z' anywhere into init. You can repeat the operation as many times as you want, and each time you can choose any position where to insert the 'z'.
For example, if init="fox", you can transform it to "fzox" in one operation. Alternately, you can transform "fox" into "zzzfoxzzz" in six operations. It is not possible to transform "fox" into any of the strings "fx", "foz", "fxo", "foxy".
Return "Yes" (quotes for clarity) if it is possible to transform init into goal. Otherwise, return "No".

Definition

Class:	InsertZ
Method:	canTransform
Parameters:	string, string
Returns:	string
Method signature:	string canTransform(string init, string goal)
(be sure your method is public)

Notes

Note that the return value is case sensitive.

Constraints

init and goal will each contain between 1 and 50 characters, inclusive.

Each character of init and goal will be a lowercase letter ('a'-'z').

init will not contain the letter 'z'.

Examples

"fox"

"fozx"

Returns: "Yes"

By inserting 'z' to the position bettween 'o' and 'x' in "fox", we obtain "fozx".

"fox"

"zfzoxzz"

Returns: "Yes"

You may perform the operation multiple times.

"foon"

"foon"

Returns: "Yes"

In this case init and goal are equal. You do not have to perform the operation.

"topcoder"

"zopzoder"

Returns: "No"

"aaaaaaaaaa"

"a"

Returns: "No"

"mvixrdnrpxowkasufnvxaq"

"mvizzxzzzrdzznzrpxozzwzzkazzzszzuzzfnvxzzzazzq"

Returns: "Yes"

"opdlfmvuicjsierjowdvnx"

"zzopzdlfmvzuicjzzsizzeijzowvznxzz"

Returns: "No"

[Thoughts]

这题即比较两个字符串，期间，如果字符为z的话，就视而不见好了。

[Code]

1:  #include <string>  
2:  #include <cstring>  
3:  using namespace std;  
4:  class InsertZ  
5:  {  
6:  public:  
7:       string canTransform(string init, string goal)  
8:       {  
9:            int i =0, j=0;  
10:            while(i<init.size() && j<goal.size())  
11:            {  
12:                 if(goal[j] == 'z')  
13:                 {  
14:                      j++;  
15:                      continue;  
16:                 }  
17:                 if(init[i]!=goal[j])  
18:                 {  
19:                      return "No";  
20:                 }  
21:                 i++;  
22:                 j++;  
23:            }  
24:            if(i<init.size())  
25:                 return "No";  
26:            while(j<goal.size())  
27:            {       
28:                 if(goal[j] != 'z')  
29:                      return "No";  
30:                 j++;  
31:            }  
32:            return "Yes";       
33:       }  
34:  };

Problem Statement 500P

Little Fox Jiro is standing at the bottom of a long flight of stairs. The bottom of the stairs has number 0, the bottommost step has number 1, the next step has number 2, and so on. The staircase is so long that Jiro is guaranteed not to reach its top.
Jiro will now perform N consecutive actions. The actions are numbered 1 through N, in order. When performing action X, Jiro chooses between two options: either he does nothing, or he jumps exactly X steps up the stairs. In other words, if Jiro starts performing action X standing on step Y, he will end it either on step Y, or on step Y+X.
For example, if N=3, Jiro will make three consecutive choices: whether or not to jump 1 step upwards, 2 steps upwards, and then 3 steps upwards.
One of the steps is broken. The number of this step is badStep. Jiro cannot jump onto this step.
You are given the ints N and badStep. Compute and return the number of the topmost step that can be reached by Jiro.

Definition

Class:	JumpFurther
Method:	furthest
Parameters:	int, int
Returns:	int
Method signature:	int furthest(int N, int badStep)
(be sure your method is public)

Constraints

N will be between 1 and 2,000, inclusive.

badStep will be between 1 and 4,000,000, inclusive.

Examples

Returns: 3

The optimal strategy is to jump upwards twice: from step 0 to step 1, and then from step 1 to step 3. This trajectory avoids the broken step.

Returns: 2

In this case step 1 is broken, so Jiro cannot jump upwards as his first action. The optimal strategy is to first stay on step 0, and then to jump from step 0 to step 2.

Returns: 5

Returns: 862641

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.

[Thoughts]
这题其实是个数学题。对于Jiro来说，最好的就是从1开始把N个step都走一遍，这样可以走的最远。但是有可能会踩到BadStep，所以如果踩到的话，那就没办法了，从2开始走，再不行，从3开始，最后总会有条路。

所以，只要找出第一个不会踩到badstep的起始路径就可以了。假设，Jiro走的路是这样，
k, k+1, k+2, ....., k+m 1<=k<=N, 0<=m<N-1

那么走的总长度就是
(k+k+m)*(m+1)/2

如果他踩到BadStep的话，那么有
（2*k+m)*(m+1）/2 = BadStep

所以，解法就出来了，固定一个k的取值，看是否存在整数m，使得Jiro踩到BadStep，有过有，则k=k+1，如果没有，k就是解，计算从k到N的总长度即可。

[Code]

1:  class JumpFurther  
2:  {  
3:  public:  
4:       int furthest(int N, int badStep)  
5:       {  
6:            int k=1;  
7:            for(; k<=N; k++)  
8:            {            
9:                 int start=0, end = N-1;  
10:                 int index=-1;  
11:                 while(start<=end)  //这里二分查找m
12:                 {  
13:                      int mid = (start+end)/2;  
14:                      int result = (2*k + mid)*(mid+1);  
15:                      if( result == 2*badStep)  
16:                      {  
17:                           index = mid;  
18:                           break;                           
19:                      }  
20:                      else if(result < 2*badStep)  
21:                      {  
22:                           start = mid+1;  
23:                      }  
24:                      else  
25:                      {  
26:                           end = mid-1;  
27:                      }  
28:                 }  
29:                 if(index == -1)  
30:                 {  
31:                      break;  
32:                 }  
33:            }  
34:            return (k+N)*(N-k+1)/2;  
35:       }  
36:  };

Problem Statement 1000P

There is a H times W rectangle divided into unit cells. The rows of cells are numbered 0 to H-1 from top to bottom, and the columns are numbered 0 to W-1 from left to right. The corners of cells are called lattice points. By definition, there are (H+1)*(W+1) lattice points in our rectangle.
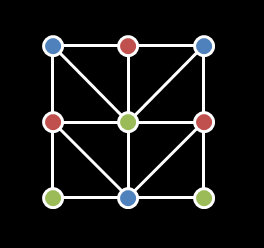
Each of the four edges of each cell is painted white. Additionally, in each cell exactly one of the two diagonals is painted white. Two lattice points are called adjacent if they are connected by a white line segment. (In other words, consecutive corners of a cell are always adjacent, opposite corners of a cell are adjacent if and only if they are connected by a painted diagonal, and no other pairs of lattice points are adjacent.)
We now want to color each of the lattice points using one of three available colors: red, green, or blue. There is only one constraint: adjacent lattice points are not allowed to share the same color.
You are given a String[] cells with H elements, each consisting of W characters. If cells[i][j] is 'N', there is a diagonal line from the top left to the bottom right corner in the cell in row i, column j. If cells[i][j] is 'Z', there is a diagonal line from the top right to the bottom left corner in the cell in row i, column j.
If there is at least one valid way to color all lattice points, return "Yes" (quotes for clarity). Otherwise, return "No".

Definition

Class:	ThreeColorabilityEasy
Method:	isColorable
Parameters:	String[]
Returns:	String
Method signature:	String isColorable(String[] cells)
(be sure your method is public)

Constraints

cells will contain between 1 and 50 elements, inclusive.

Each element of cells will contain between 1 and 50 characters, inclusive.

All elements of cells will contain the same number of characters.

Each character of cells will be either 'N' or 'Z'.

Examples

{"Z"}

Returns: "Yes"

One of the possible colorings is as follows.

{"NZ"
,"NZ"}

Returns: "Yes"

{"ZZZ"
,"ZNZ"}

Returns: "No"

{"NZNZNNN"
,"NNZNNNZ"
,"NNNNZZZ"
,"ZZZNZZN"
,"ZZNZNNN"
,"NZZZZNN"
,"ZZZNZNN"}

Returns: "No"

{"ZZZZ"
,"ZZZZ"
,"ZZZZ"}

Returns: "Yes"

[Thoughts]
刚看到这个题的第一个想法就是，这不是图的m着色问题吗？回溯遍历解空间就好了。但是这个题有个简化在于，它是严格的矩形，而且每一个格子里面只能有一个对角线。

对于这种可能存在对称的图，挑个例子看一下就好了，比如四个格子，如上图，只有三种布局可能：
1. 全部一样的对角线
2. 两两相同的对角线
3. 三个格子对角线相同

如图示，对于#1及#2，都可以很容易找到解。但是对于第三种情况，总会有个点最后没法染色，因为它的周边已经被三种颜色渲染了。

所以落到这一题里面，只要在格子中找，是否存在第三种布局就好了。

[Code]

1:  #include <string>  
2:  #include <vector>  
3:  using namespace std;  
4:  class ThreeColorabilityEasy  
5:  {  
6:  public:  
7:       string isColorable(vector <string> cells)  
8:       {  
9:            int row = cells.size();  
10:            int col = cells[0].size();  
11:            if(row == 1 || col ==1) return "Yes";  
12:            for(int i =0; i<row-1; i++)  
13:            {                 
14:                 for(int j=0; j<col-1; j++)  
15:                 {  
16:                      int count=0;  
17:                      if(cells[i][j] == 'N') count++;  
18:                      if(cells[i][j+1] == 'N') count++;  
19:                      if(cells[i+1][j] == 'N') count++;  
20:                      if(cells[i+1][j+1] == 'N') count++;  
21:                      if(count ==1 || count ==3) return "No";  
22:                 }  
23:            }  
24:            return "Yes";  
25:       }  
26:  };

水中的鱼

Friday, August 2, 2013

[TopCoder] SRM 587 DIV 2, 250p, 500p, 1000p, Solution

Problem Statement 250P

Definition

Notes

Constraints

Examples

Problem Statement 500P

Definition

Constraints

Examples

Problem Statement 1000P

Definition

Constraints

Examples

No comments: